【花雕动手做】Kitronik 可编程游戏开发板基于 ARCADE MakeCode 之Pi 蒙特卡洛游戏 简单

Kitronik ARCADE 是一款由英国教育科技公司 Kitronik 精心打造的可编程游戏机开发板，专为编程教学与创客实践而设计。该设备原生支持微软的 MakeCode Arcade 平台，用户可通过图形化或 JavaScript 编程方式，轻松创建、下载并运行复古风格的街机游戏。

它集成了彩色 LCD 显示屏、方向控制键、功能按键、蜂鸣器和震动马达等交互组件，提供完整的游戏输入输出体验。无论是初学者进行编程启蒙，还是创客群体开发交互式作品，Kitronik ARCADE 都能作为理想的硬件载体，助力创意实现。

凭借其开源友好、易于上手、兼容性强等特点，该开发板广泛应用于中小学编程课程、创客工作坊、游戏开发教学以及个人项目原型设计，深受教育者与技术爱好者的喜爱。

作为学习、练习与尝试，这里创建一个Pi 蒙特卡洛的小游戏。
打开网页版：https://arcade.makecode.com/，设置项目名称：Pi 蒙特卡洛

MicroPython实验代码

ARCADE MakeCode Pi 蒙特卡洛游戏代码解读
这是一个使用蒙特卡洛方法估算π值的游戏程序。代码结构分析：

1. 自定义精灵类型
python
class SpriteKind:
   Square = SpriteKind.create()
   Circle = SpriteKind.create()
定义两种精灵类型：方形和圆形，用于表示蒙特卡洛模拟中的方形区域和圆形区域。

2. 全局变量初始化
python
# 各种变量初始化
delay2 = 0
simulate = False
j = 0
yy = 0
xx = 0
squareDots = 0  # 方形内的点数
circleDots = 0  # 圆形内的点数
mCircle: Sprite = None
mSquare: Sprite = None
cirImage: Image = None
dots = 0
r = 0

# 设置形状的半径和边长
r = scene.screen_height() / 4  # 半径为屏幕高度的1/4
l = r * 2 + 1  # 方形边长

# 总点数（样本数量）
dots = 1000000

# 虚拟半径长度（用于计算）
r2 = 5000

# 实际半径与虚拟半径的比例
scale = (r + 1) / r2
3. 图像和精灵创建
python
# 创建方形图像
sqImage = image.create(l, l)
sqImage.fill(0)
sqImage.draw_rect(0, 0, l, l, 1)

# 创建圆形图像
cirImage = image.create(l, l)
cirImage.fill(0)

# 显示游戏介绍
game.splash("Approximate Pi", "Monte Carlo Method")

# 创建方形精灵
mSquare = sprites.create(sqImage, SpriteKind.Square)
mSquare.set_flag(SpriteFlag.AUTO_DESTROY, True)

# 绘制圆形轮廓
drawCircle()

# 创建圆形精灵
mCircle = sprites.create(cirImage, SpriteKind.Circle)
4. 绘制圆形函数
python
def drawCircle():
   global xx, yy
   # 使用随机点绘制圆形轮廓
   for index in range(dots):
       xx = randint(0, 2 * r) - r
       yy = randint(0, 2 * r) - r
       # 测试点是否在圆形轮廓上
       if xx * xx + yy * yy >= r ** 2 and xx * xx + yy * yy < (r + 1) ** 2:
           cirImage.set_pixel(xx + r, yy + r, 1)
5. 蒙特卡洛模拟主循环
python
def on_forever():
   global xx, yy, squareDots, circleDots, j
   # 简单的蒙特卡洛模拟来估算π值
   while j < dots and simulate:
       # 在方形内生成随机点
       xx = randint(0, 2 * r2) - r2
       yy = randint(0, 2 * r2) - r2
       sqImage.set_pixel(xx * scale + r, yy * scale + r, 7)
       squareDots += 1
       
       # 测试点是否在圆形内
       if xx * xx + yy * yy <= r2 ** 2:
           circleDots += 1
           # 缩放到屏幕坐标
           xx = xx * scale
           yy = yy * scale
           # 调整x或y为0的位置
           if xx < 0:
               xx += 1
           if yy < 0:
               yy += 1
           cirImage.set_pixel(xx + r, yy + r, 2)
       
       # 定期更新显示
       if squareDots < dots / 50 and squareDots % 100 == 0:
           info.set_score(circleDots)
           pause(100)
       
       j += 1
       
       # 完成模拟
       if j >= dots:
           info.set_score(circleDots)
           info.set_life(0)
6. 更新间隔函数
python
def on_update_interval():
   global simulate, delay2
   if delay2 > 10:
       # 开始模拟
       simulate = True
   if delay2 > 20:
       # 将形状分开
       if mCircle.x < scene.screen_width() - 3 * r / 2:
           mSquare.x += -1
           mCircle.x += 1
   delay2 += 1
7. 事件处理函数
python
# B按钮按下事件：显示π值估算结果
def on_b_pressed():
   game.show_long_text("Pi: " + ("" + str(4 * circleDots / squareDots)) + " using " + ("" + str(circleDots)) + " dots",
       DialogLayout.BOTTOM)
controller.B.on_event(ControllerButtonEvent.PRESSED, on_b_pressed)

# 生命值为零事件：显示最终结果
def on_life_zero():
   info.set_score(circleDots)
   game.show_long_text("Pi: " + ("" + str(4 * circleDots / squareDots)),
       DialogLayout.BOTTOM)
   mCircle.say("Bye..")
   mCircle.vx = 1000
   mSquare.say("..we have Pi")
   mSquare.ax = 50
info.on_life_zero(on_life_zero)

# 方形精灵销毁事件：重置游戏
def on_on_destroyed(sprite):
   game.reset()
sprites.on_destroyed(SpriteKind.Square, on_on_destroyed)
蒙特卡洛方法原理
这个程序使用蒙特卡洛方法估算π值，原理如下：

在一个正方形内随机生成大量点

统计落在内切圆内的点的数量

根据公式 π ≈ 4 × (圆内点数 / 总点数) 估算π值

这种方法通过随机抽样和概率统计来近似计算数学常数，是蒙特卡洛方法的经典应用。

这个程序通过可视化方式展示了这一过程，使抽象的数学概念变得更加直观和有趣。

图形编程参考实验程序

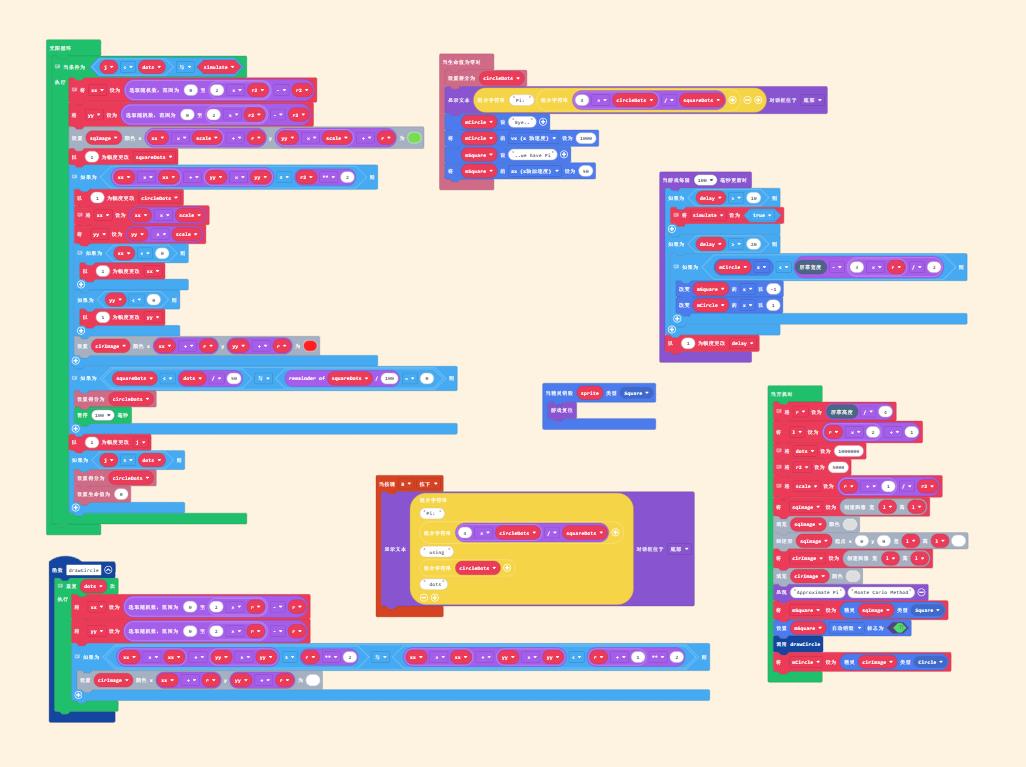
通过模拟器，调试与模拟运行

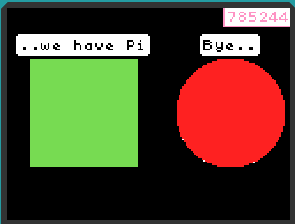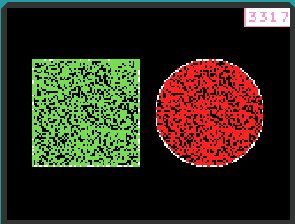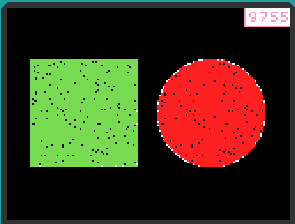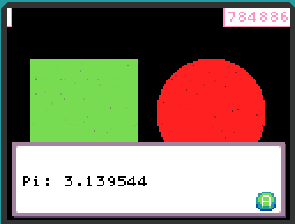
实验场景记录