一、项目背景
在日常生活中,我们经常需要将物品进行包装或存放。从环保的角度思考使用A4纸大小的木板(3mm厚)制作一个既实用又美观的存储盒子,然而,如何设计才能使盒子的体积最大,这是一个有趣的挑战。通过本次项目,我们将探讨这个问题,并利用数学和工程设计的知识来寻找解决方案。
二、项目目标
利用回收的木板材料,减少环境负担,最大化木板的使用效率,不浪费任何可用空间。
掌握盒子的体积计算公式。
通过实践,找到使盒子体积最大的最佳方法。
培养团队合作、创新思维和实践能力。
三、实施步骤
准备阶段:先以A4纸为例子,收集有关纸张折叠和几何图形体积计算的相关知识。了解如何使用A4纸折叠出不同形状的盒子。
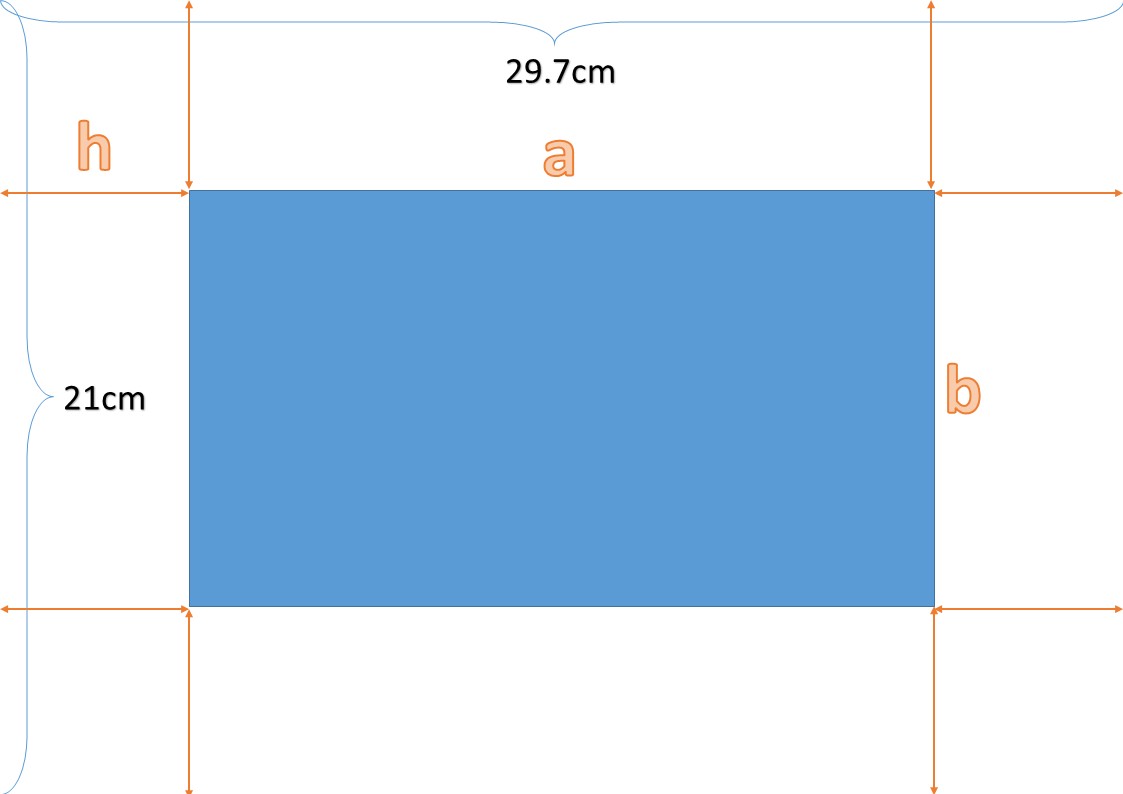
【 设计阶段】:根据所学知识,设计并绘制不同形状的盒子草图。记录下每种设计的体积计算公式。
研究方法:通过测量,A4纸的长宽分别约是29和21。会发现最简单的是截取4个角上的4个正方形。那个正方形的边长是做好后长方体的高。于是得到了以下几个关系式:
设做好后长方体长为a,宽为b,高为c:
则a+2c=29,且b+2c=21,
∴a-b=8,b=21-2c
列出表格:
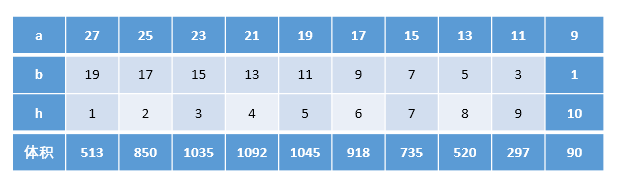
会发现,当4<c<5时,这个无盖长方体盒子的体积最大。具体哪个值最合适呢?我们继续推理。
推理公式
设的长为a,宽为b,高为h,
已知b+2c=29,a+2c=21→b=29-2c,a=21-2c
V为无盖长方体的体积
V(长方体)=abc
∴V=a·b·c=(21-2c)(29-2c)·c
【模拟阶段】:做为小学生如何解决这个问题呢?可以编程的方法设计:

下面是呈现的结果。
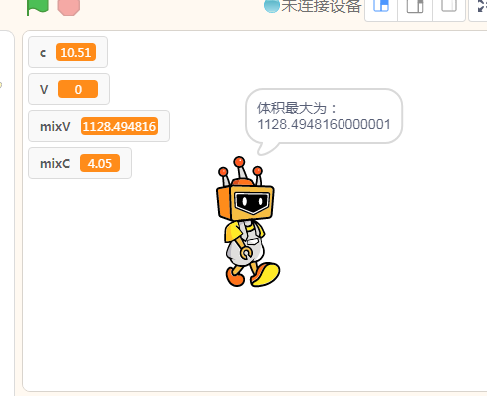
在运行过程中增加了等待目的是运行过程中孩子们能观察到高度与体积之间的变化过程。
【模型设计阶段】:根据模拟结果,选择具有最大体积的盒子设计。使用LaserMaker对盒子进行设计
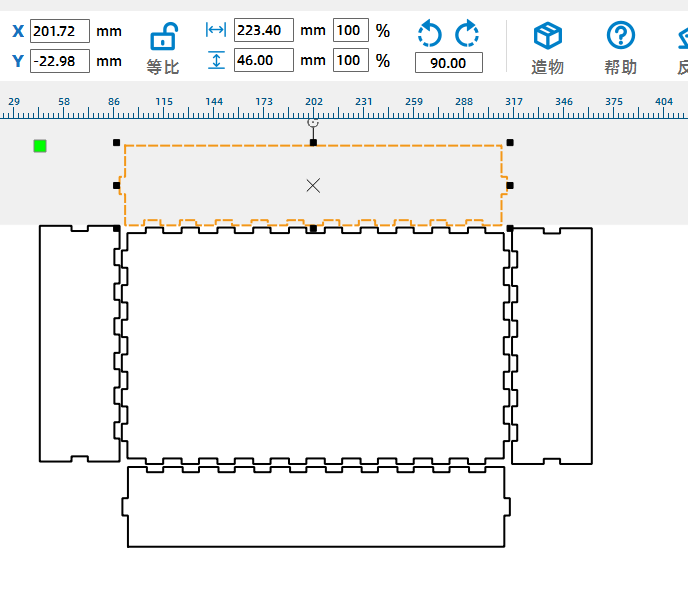
因为用了3cm的木板进行切割,还需要考虑其厚度和激光切割的补偿。
【切割阶段】:切割好后进行安装并总结经验和教训。

【应用阶段】:将所得结论应用到实际生活中,例如包装礼物、制作储物盒等。发挥创造力,将所学知识应用到实际问题的解决中。
四、注意事项
在进行体积计算时,要确保计算公式正确无误。
在团队合作中,要充分发挥每个人的优势,共同解决问题。
在整个过程中,要注重实践与理论相结合,不断提升技能和能力。

 返回首页
返回首页
 回到顶部
回到顶部





评论